Yeah, but they're also just symbols - if it had've been √2 you meant then you may also have been leaving the -1 separate from the 3 to make it clear how you were manipulating the equation.mcminty wrote:
How can you say "exactly" to that??Scorpion0x17 wrote:
Exactly.mcminty wrote:
also commonly known as √2...
If I had written √3-1 as meaning the "square root of 3-minus-1", then I would have written √2. So I must have meant "the square root of 3, minus 1".
How is that confusing at all?
And that style of √, could lead to confusion - what's √3-a ? is it "the square root of 3, minus a"? or "the square root of 3-minus-a"?
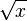 is the same as √x
is the same as √x

