yeah this is just General Physics IScorpion0x17 wrote:
Are we talking Newtonian or Einsteinian physics?
'Cos if it's the later, all your answers are wrong.
But I'm guessing it's the former.
To solve the gazelle one, integrate the acceleration function twice to get 1.85x2. Set this equal to 60, and solve for x. Plug this x value into 3.7x, the velocity function, to get the final speed.
This should be right. I can't solve it without calculus, sorry.
Edit: Free answer check. The answer is 21.053. Sorry, didn't notice it had been solved. If you knew calculus, that would be the way to do it.
This should be right. I can't solve it without calculus, sorry.
Edit: Free answer check. The answer is 21.053. Sorry, didn't notice it had been solved. If you knew calculus, that would be the way to do it.
Last edited by nukchebi0 (2009-01-18 21:00:10)
People not getting sarcasm happens all too often around here too.Defiance wrote:
This is all Physics 101, did you really need to ask or are you just looking to argue with someone?Scorpion0x17 wrote:
Are we talking Newtonian or Einsteinian physics?
'Cos if it's the later, all your answers are wrong.
But I'm guessing it's the former.
Happens too often around here.
I got another problem that I need help and here's the question:
1) A balloon is rising at 12 m/s when its passenger throws a ball straight up at 28 m/s. How much later does the passenger catch the ball?
I'm sort of confused on this one because what does the balloon have to do with the ball? Also am I suppose to use this equation y=1/2gt^2 or not?
1) A balloon is rising at 12 m/s when its passenger throws a ball straight up at 28 m/s. How much later does the passenger catch the ball?
I'm sort of confused on this one because what does the balloon have to do with the ball? Also am I suppose to use this equation y=1/2gt^2 or not?
Point is that the balloon continues to raise at 12m/s but the ball starts to deaccelerate at 9.81m/s^2 before it starts falling down.TheunforgivenII wrote:
I got another problem that I need help and here's the question:
1) A balloon is rising at 12 m/s when its passenger throws a ball straight up at 28 m/s. How much later does the passenger catch the ball?
I'm sort of confused on this one because what does the balloon have to do with the ball? Also am I suppose to use this equation y=1/2gt^2 or not?
You can solve that using a vertical projectile motion equation on the ball..TheunforgivenII wrote:
I got another problem that I need help and here's the question:
1) A balloon is rising at 12 m/s when its passenger throws a ball straight up at 28 m/s. How much later does the passenger catch the ball?
I'm sort of confused on this one because what does the balloon have to do with the ball? Also am I suppose to use this equation y=1/2gt^2 or not?
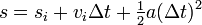
Ok, so SB is the position of the Balloon, and Sba is the position of the Ball. For simplicity, we'll assume that the initial position (Si) is 0. We are given the initial velocities in the question, and we know that a = -9.81 m/s/s (acceleration due to gravity).
Now generate equations for SB and Sbl.
SB = 12 m/s x t (ie. distance balloon travels upwards after t seconds, if its velocity is 12m/s)
SB = 12t
Sbl = 28m/s x t + 1/2 x -9.81 x t2
Sbl = 28t - 4.9t2
We want to equate SB and Sbl, that is assume that the position of the ball and balloon are the same (when the passanger cathces the ball!). We'll be able to find a quadratic and solve for t.
SB = Sbl
12t = 28t - 4.9t2
- 4.9t2 + 16t = 0
Sub into:

This yields t = 0 (true from beginning) and t = 3.265s. That should be it.
use y=12t for the balloon andGawwad wrote:
Point is that the balloon continues to raise at 12m/s but the ball starts to deaccelerate at 9.81m/s^2 before it starts falling down.TheunforgivenII wrote:
I got another problem that I need help and here's the question:
1) A balloon is rising at 12 m/s when its passenger throws a ball straight up at 28 m/s. How much later does the passenger catch the ball?
I'm sort of confused on this one because what does the balloon have to do with the ball? Also am I suppose to use this equation y=1/2gt^2 or not?
y=(12+28)t+.5gt2
FUCK.argo4 wrote:
y=(12+28)t+.5gt2
It's 3:30am here. I cbf to change my above post. Same idea tho.
EDIT: Lol, I'm rather at the moment. Heh, always hated physics..
thanks mcminty, I understand nowmcminty wrote:
You can solve that using a vertical projectile motion equation on the ball..TheunforgivenII wrote:
I got another problem that I need help and here's the question:
1) A balloon is rising at 12 m/s when its passenger throws a ball straight up at 28 m/s. How much later does the passenger catch the ball?
I'm sort of confused on this one because what does the balloon have to do with the ball? Also am I suppose to use this equation y=1/2gt^2 or not?
http://upload.wikimedia.org/math/3/0/f/ … af26aa.png
Ok, so SB is the position of the Balloon, and Sba is the position of the Ball. For simplicity, we'll assume that the initial position (Si) is 0. We are given the initial velocities in the question, and we know that a = -9.81 m/s/s (acceleration due to gravity).
Now generate equations for SB and Sbl.
SB = 12 m/s x t (ie. distance balloon travels upwards after t seconds, if its velocity is 12m/s)
SB = 12t
Sbl = 28m/s x t + 1/2 x -9.81 x t2
Sbl = 28t - 4.9t2
We want to equate SB and Sbl, that is assume that the position of the ball and balloon are the same (when the passanger cathces the ball!). We'll be able to find a quadratic and solve for t.
SB = Sbl
12t = 28t - 4.9t2
- 4.9t2 + 16t = 0
Sub into:
http://upload.wikimedia.org/math/8/c/5/ … b0e91a.png
This yields t = 0 (true from beginning) and t = 3.265s. That should be it.
haha,no worries, i'm in the middle of studying for ap physics somcminty wrote:
FUCK.argo4 wrote:
y=(12+28)t+.5gt2
It's 3:30am here. I cbf to change my above post. Same idea tho.
EDIT: Lol, I'm rather at the moment. Heh, always hated physics..
I was just looking through some forums for Physics and this one popped up.....and I really need help on a couple of confusing problems that I cannot get.
1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
I'm confused on this one because I do not understand what x = bt^2 comes from
1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
I'm confused on this one because I do not understand what x = bt^2 comes from
I'm pretty sure x = meters traveled.Sheen1101 wrote:
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
I'm confused on this one because I do not understand what x = bt^2 comes from
So for half way it would be 200m = 2.200m/s^2 * t^2 leaving only t as unknown.
so i just solve for tGawwad wrote:
I'm pretty sure x = meters traveled.Sheen1101 wrote:
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
I'm confused on this one because I do not understand what x = bt^2 comes from
So for half way it would be 200m = 2.200m/s^2 * t^2 leaving only t as unknown.
haha, i would help, but my physics midterm is over so lol no more physics for meSheen1101 wrote:
I was just looking through some forums for Physics and this one popped up.....and I really need help on a couple of confusing problems that I cannot get.
1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
I'm confused on this one because I do not understand what x = bt^2 comes from
ha-haargo4 wrote:
haha, i would help, but my physics midterm is over so lol no more physics for meSheen1101 wrote:
I was just looking through some forums for Physics and this one popped up.....and I really need help on a couple of confusing problems that I cannot get.
1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
I'm confused on this one because I do not understand what x = bt^2 comes from
me too, but we're not really studying the same materialSheen1101 wrote:
ha-haargo4 wrote:
haha, i would help, but my physics midterm is over so lol no more physics for meSheen1101 wrote:
I was just looking through some forums for Physics and this one popped up.....and I really need help on a couple of confusing problems that I cannot get.
1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
I'm confused on this one because I do not understand what x = bt^2 comes from
"people in ny have a general idea of how to drive. one of the pedals goes forward the other one prevents you from dying"
Still trying to get my head round all this peculiar baseball stuff.
Get change in position:
x1 = 178m
x2 = 222m
dx = x2 - x1 = 222 - 178 = 44
Rearrange x = bt2 for t:
t = sqrt(x/b) where b = acceleration
Time at x1 = t1 = sqrt(x1/b) = 10.045
Time at x2 = t2 = sqrt(x2/b) = 8.995
dt = t2 - t1 = 1.05
v = dx/dt = 44/1.05 = 41.9ms-1
(b)
Using (where b = a = acceleration):
v2 = u2 + 2as
v = sqrt(2as)
v = sqrt(2*2.2*200) = 29.66
Percentage difference is about 40%.
(a)Sheen1101 wrote:
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
Get change in position:
x1 = 178m
x2 = 222m
dx = x2 - x1 = 222 - 178 = 44
Rearrange x = bt2 for t:
t = sqrt(x/b) where b = acceleration
Time at x1 = t1 = sqrt(x1/b) = 10.045
Time at x2 = t2 = sqrt(x2/b) = 8.995
dt = t2 - t1 = 1.05
v = dx/dt = 44/1.05 = 41.9ms-1
(b)
Using (where b = a = acceleration):
v2 = u2 + 2as
v = sqrt(2as)
v = sqrt(2*2.2*200) = 29.66
Percentage difference is about 40%.
I got to this part but then couldn't finish.....my professor explained it to me in class but couldn't understand because I also couldn't understand what she was talking about. I just can't hear her words because of her deep Russian accent and poor englishliquidat0r wrote:
Still trying to get my head round all this peculiar baseball stuff.(a)Sheen1101 wrote:
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
Get change in position:
x1 = 178m
x2 = 222m
dx = x2 - x1 = 222 - 178 = 44
Rearrange x = bt2 for t:
t = sqrt(x/b) where b = acceleration
Time at x1 = t1 = sqrt(x1/b) = 10.045
Time at x2 = t2 = sqrt(x2/b) = 8.995
Well I presume that in question 1:
- Travel from the pitcher to the catcher: 67ft divided by 90mph (but with units converted)
- Be re-thrown by the catcher: 0.45s
- Travel from the catcher to <somewhere, I don't know baseball> ... time = distance divided by velocity
Has to be less than 3.43s to make an out.
So the only unknown in the equation formed there is the velocity of the ball as it is thrown by the catcher. Rearrange and solve.
You'll need to convert to SI units, or at least common units (miles per second, feet per hour, miles per hour, etc), to solve it.
The total time taken for the ball to:1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
- Travel from the pitcher to the catcher: 67ft divided by 90mph (but with units converted)
- Be re-thrown by the catcher: 0.45s
- Travel from the catcher to <somewhere, I don't know baseball> ... time = distance divided by velocity
Has to be less than 3.43s to make an out.
So the only unknown in the equation formed there is the velocity of the ball as it is thrown by the catcher. Rearrange and solve.
You'll need to convert to SI units, or at least common units (miles per second, feet per hour, miles per hour, etc), to solve it.
Last edited by liquidat0r (2009-01-21 16:35:48)
Assuming that you understand up to the point where you trimmed the quote.Sheen1101 wrote:
I got to this part but then couldn't finish.....my professor explained it to me in class but couldn't understand because I also couldn't understand what she was talking about. I just can't hear her words because of her deep Russian accent and poor english
You now have a change in position and a change in time.
Velocity is defined as the change in position per unit time. i.e. v = dx/dt
So you're just dividing dx by dt ...
Yeah I understand how to do that part now...i was over thinking on most of the problem which confused meliquidat0r wrote:
Assuming that you understand up to the point where you trimmed the quote.Sheen1101 wrote:
I got to this part but then couldn't finish.....my professor explained it to me in class but couldn't understand because I also couldn't understand what she was talking about. I just can't hear her words because of her deep Russian accent and poor english
You now have a change in position and a change in time.
Velocity is defined as the change in position per unit time. i.e. v = dx/dt
So you're just dividing dx by dt ...
Some culturing would do you good liq.liquidat0r wrote:
Still trying to get my head round all this peculiar baseball stuff.
Anyway, fairly straightforward problem.
First, convert to feet/sec. Which means multiply by 5280/3600, or 1.466667. The pitcher throws the ball 67 feet at 132 feet per second. It took him a total of 0.507576 seconds to get the ball to the catcher. Add that to the .45s of transfer from a catcher (not that impressive tbh), and you get .957576 seconds until the catcher releases the ball. 3.43s - .957576 = 2.472424 seconds for the catcher to get the ball to second. A baseball diamond is 90ft from each base to base, so the diagonal from the plate to 2nd is 90ft*the square root of 2, or 127.27922ft. Naturally, the catcher has to throw the ball at 51.479528 feet/sec. Convert back to MPH... multiply by the inverse of what we did earlier. You get 35.09968, or 35.1mph. (which is stupidly slow).1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
However, the dumb problem doesn't take into account that the runner leaves in the middle of the pitcher's delivery, far from when he releases the ball. Any runner dumb enough to leave then is going to be toasted. 3.5 seconds isn't super quick, and it also doesn't take into account any lead the runner might have.
tldr; if you're a catcher and think you can throw anybody out with a 35mph ball, you're absolutely wrong.
whoa that a lot of work and conversions....now it's my turn to read and study all thatMadKatter wrote:
Some culturing would do you good liq.liquidat0r wrote:
Still trying to get my head round all this peculiar baseball stuff.
Anyway, fairly straightforward problem.First, convert to feet/sec. Which means multiply by 5280/3600, or 1.466667. The pitcher throws the ball 67 feet at 132 feet per second. It took him a total of 0.507576 seconds to get the ball to the catcher. Add that to the .45s of transfer from a catcher (not that impressive tbh), and you get .957576 seconds until the catcher releases the ball. 3.43s - .957576 = 2.472424 seconds for the catcher to get the ball to second. A baseball diamond is 90ft from each base to base, so the diagonal from the plate to 2nd is 90ft*the square root of 2, or 127.27922ft. Naturally, the catcher has to throw the ball at 51.479528 feet/sec. Convert back to MPH... multiply by the inverse of what we did earlier. You get 35.09968, or 35.1mph. (which is stupidly slow).1) A fast base-runner can get from first to second base in 3.43 s. If he leaves first base as the pitcher throws a 90 mi/h fastball the 67-ft distance to the catcher, and if the catcher takes 0.45 s to catch and re-throw the ball, how fast does the catcher have to throw the ball to second base to make an out? Home plate to second base is the diagonal of a square 90 ft on a side.
~the answer has to be in miles per hour
However, the dumb problem doesn't take into account that the runner leaves in the middle of the pitcher's delivery, far from when he releases the ball. Any runner dumb enough to leave then is going to be toasted. 3.5 seconds isn't super quick, and it also doesn't take into account any lead the runner might have.
tldr; if you're a catcher and think you can throw anybody out with a 35mph ball, you're absolutely wrong.
~Thanks for the help!
NP... it's not actually that much, it just looks bad because I left a load of decimals.
The process is pretty simple.
Convert the pitching speed
Measure the time it takes for the ball to get to the catcher
add to catcher's transfer speed
then subtract the total from the time it takes for the runner to steal.
Now that you have time, you only need distance, which you get by knowing your triangle side-laws. Right triangles with 2 equal sides have a hypotenuse of one equal side * the square root of 2, you should probably know this.
Divide
Re-convert.
:p
The process is pretty simple.
Convert the pitching speed
Measure the time it takes for the ball to get to the catcher
add to catcher's transfer speed
then subtract the total from the time it takes for the runner to steal.
Now that you have time, you only need distance, which you get by knowing your triangle side-laws. Right triangles with 2 equal sides have a hypotenuse of one equal side * the square root of 2, you should probably know this.
Divide
Re-convert.
:p
I do not understand how you got the percentage difference about 40%? I typed that in for my answer at first into WebAssign and it was wrong. I only have 10 chances to get the answer correct but I've been trying to figure it out and now I have 8/10 chances leftliquidat0r wrote:
Still trying to get my head round all this peculiar baseball stuff.(a)Sheen1101 wrote:
2) In a drag race, the position of a car as a function of time is given by x = bt^2, with b = 2.200 m/s^2. In an attempt to determine the car's velocity midway down a 400 m track, two observers stand at the 178 m and 222 m marks and note the time when the car passes them.
(a) What value do the two observers compute for the car's velocity? Give your answer to four significant figures.
(b) By what percentage does this observed value differ from the actual instantaneous value at x = 200 m?
Get change in position:
x1 = 178m
x2 = 222m
dx = x2 - x1 = 222 - 178 = 44
Rearrange x = bt2 for t:
t = sqrt(x/b) where b = acceleration
Time at x1 = t1 = sqrt(x1/b) = 10.045
Time at x2 = t2 = sqrt(x2/b) = 8.995
dt = t2 - t1 = 1.05
v = dx/dt = 44/1.05 = 41.9ms-1
(b)
Using (where b = a = acceleration):
v2 = u2 + 2as
v = sqrt(2as)
v = sqrt(2*2.2*200) = 29.66
Percentage difference is about 40%.